
|
The ancient philosopher, Heraclitus,
maintained that everything is in a state of flux. Nothing escapes change
of some sort (it is impossible to step into the same river). On the other
hand, Parmenides argued that everything is what it is, so that it cannot
become what is not (change is impossible because a substance would have to
transition through nothing to become something else, which is a logical
contradiction). Thus, change is incompatible with being so that only the
permanent aspects of the Universe could be considered real.
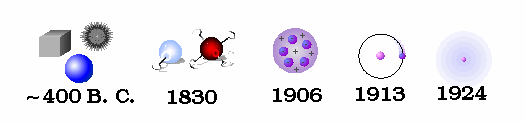
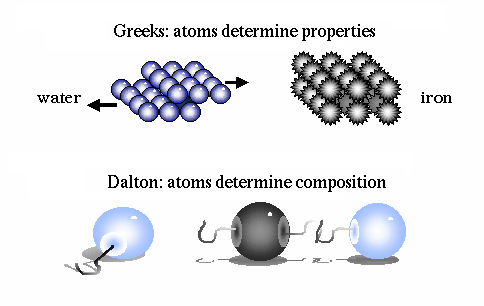
.. An ingenious escape was proposed in the fifth century B.C. by Democritus. He hypothesized that all matter (plus space and time) is composed of tiny indestructible units, called atoms. This idea seems motivated by the question of how finely one can go on cutting up matter. While Democritus performed no experiments and had only the flimsiest evidence for postulating the existence of atoms, his theory was kept alive by the Roman poet Lucretius which survived the Dark Ages to be discovered in 1417. The atoms in Democritus theory themselves remain unchanged, but move about in space to combine in various ways to form all macroscopic objects. Early atomic theory stated that the characteristics of an object are determined by the shape of its atoms. So, for example, sweet things are made of smooth atoms, bitter things are made of sharp atoms. .. In this manner permanence and flux are reconciled and the field of atomic physics was born. Although Democritus' ideas were to solve a philosophical dilemma, the fact that there is some underlying, elemental substance to the Universe is a primary driver in modern physics, the search for the ultimate subatomic particle. |
.. |
.. It was John Dalton, in the early 1800's, who determined that each chemical element is composed of a unique type of atom, and that the atoms differed by their masses. He devised a system of chemical symbols and, having ascertained the relative weights of atoms, arranged them into a table. In addition, he formulated the theory that a chemical combination of different elements occurs in simple numerical ratios by weight, which led to the development of the laws of definite and multiple proportions. .. He then determined that compounds are made of molecules, and that molecules are composed of atoms in definite proportions. Thus, atoms determine the composition of matter, and compounds can be broken down into their individual elements. |
.. |
.. The first estimates for the sizes of atoms and the number of atoms per unit volume where made by Joesph Loschmidt in 1865. Using the ideas of kinetic theory, the idea that the properties of a gas are due to the motion of the atoms that compose it, Loschmidt calculated the mean free path of an atom based on diffusion rates. His result was that there are 6.022x1023 atoms per 12 grams of carbon. And that the typical diameter of an atom is 10-8 centimeters. |
|
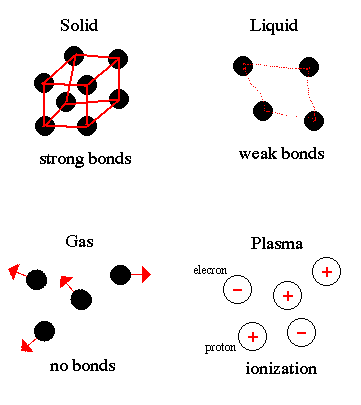
Matter exists in four states: solid, liquid, gas and plasma. Plasmas are only found in the coronae and cores of stars. The state of matter is determined by the strength of the bonds between the atoms that makes up matter. Thus, is proportional to the temperature or the amount of energy contained by the matter. |
.. |
.. The change from one state of matter to another is called a phase transition. For example, ice (solid water) converts (melts) into liquid water as energy is added. Continue adding energy and the water boils to steam (gaseous water) then, at several million degrees, breaks down into its component atoms. |
.. |
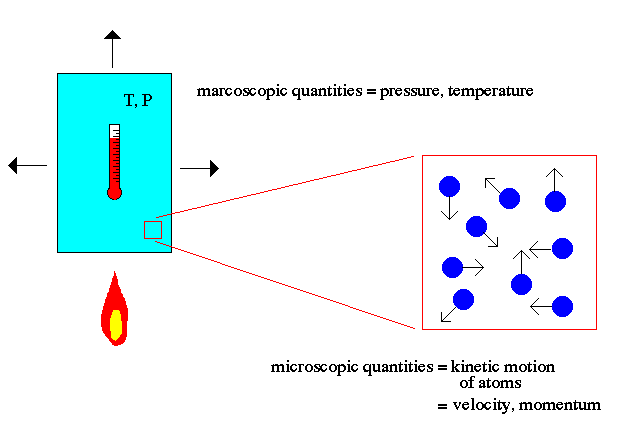
.. Atomic theory is the field of physics that describes the characteristics and properties of atoms that make up matter. The key point to note about atomic theory is the relationship between the macroscopic world (us) and the microscopic world of atoms. For example, the macroscopic world deals with concepts such as temperature and pressure to describe matter. The microscopic world of atomic theory deals with the kinetic motion of atoms to explain macroscopic quantities. .. Temperature is explained in atomic theory as the motion of the atoms (faster = hotter). Pressure is explained as the momentum transfer of those moving atoms on the walls of the container (faster atoms = higher temperature = more momentum/hits = higher pressure). |
|
Macroscopic properties of matter are
governed by the Ideal Gas
Law of chemistry.
.. An ideal gas is a gas that conforms, in physical behavior, to a particular, idealized relation between pressure, volume, and temperature. The ideal gas law is a generalization containing both Boyle's law and Charles's law as special cases and states that for a specified quantity of gas, the product of the volume, V, and pressure, P, is proportional to the absolute temperature T; i.e., in equation form, PV = kT, in which k is a constant. Such a relation for a substance is called its equation of state and is sufficient to describe its gross behavior. .. The ideal gas law can be derived from the kinetic theory of gases and relies on the assumptions that (1) the gas consists of a large number of molecules, which are in random motion and obey Newton's laws of motion; (2) the volume of the molecules is negligible small compared to the volume occupied by the gas; and (3) no forces act on the molecules except during elastic collisions of negligible duration. .. Although no gas has these properties, the behavior of real gases is described quite closely by the ideal gas law at sufficiently high temperatures and low pressures, when relatively large distances between molecules and their high speeds overcome any interaction. A gas does not obey the equation when conditions are such that the gas, or any of the component gases in a mixture, is near its condensation point. .. The ideal gas law may be written in a form applicable to any gas, according to Avogadro's law (q.v.), if the constant specifying the quantity of gas is expressed in terms of the number of molecules of gas. This is done by using as the mass unit the gram-mole; i.e., the molecular weight expressed in grams. The equation of state of n gram-moles of a perfect gas can then be written as pv/t = nR, in which R is called the universal gas constant. This constant has been measured for various gases under nearly ideal conditions of high temperatures and low pressures, and it is found to have the same value for all gases: R = 8.314 joules per gram-mole-kelvin. |
.. |
.. Although no gas is perfectly described by the above laws, the behavior of real gases is described quite closely by the ideal gas law at sufficiently high temperatures and low pressures (such as air pressure at sea level), when relatively large distances between molecules and their high speeds overcome any interaction. A gas does not obey the equation when conditions are such that the gas, or any of the component gases in a mixture, is near its triple point (see below). |
.. |
.. The ideal gas law can be derived from the kinetic theory of gases and relies on the assumptions that (1) the gas consists of a large number of molecules, which are in random motion and obey Newton's deterministic laws of motion; (2) the volume of the molecules is negligible small compared to the volume occupied by the gas; and (3) no forces act on the molecules except during elastic collisions of negligible duration. .. While all the above conditions are not strictly true, (where they breakdown interesting things happen - such as friction) in general the behavior of matter is well described by this kinetic theory. Temperature is explained by atomic theory as the motion of the atoms (faster = hotter). Pressure is explained as the momentum transfer of those moving atoms on the walls of the container (faster atoms = higher temperature = more momentum/hits = higher pressure). |
|
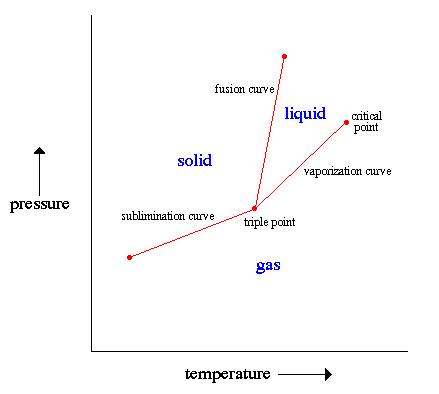
The states of matter for a substance are determined by both its temperature and its internal pressure. A fast graphic way to display the various states is called a phase diagram. A phase diagram is a graph showing the limiting conditions for solid, liquid, and gaseous phases of a single substance or of a mixture of substances while undergoing changes in pressure and temperature or in some other combination of variables, such as solubility and temperature. The figure shown below displays a typical phase diagram for a one-component system (i.e., one consisting of a single pure substance), the curves having been obtained from measurements made at various pressures and temperatures. |
.. |
.. At any point in the areas separated by the curves, the pressure and temperature allow only one phase (solid, liquid, or gas) to exist, and changes in temperature and pressure, up to the points on the curves, will not alter this phase. At any point on the curves, the temperature and pressure allow two phases to exist in equilibrium: solid and liquid, solid and gas, or liquid and gas. .. For example, the line drawn for the variation with temperature of gas pressure for the liquid is the boundary between liquid and gas; only gas can exist on the low-pressure, high-temperature side of the line, while the substance must be liquid on the high-pressure, low-temperature side; liquid and gas exist together at temperatures and pressures corresponding to points on the line; at the place where this line vanishes, called the critical point, the liquid and its gas become indistinguishable. Along the line between liquid and solid, the melting temperatures for different pressures can be found. The junction of the three curves, called the triple point, represents the unique conditions under which all three phases exist in equilibrium together. .. A substance triple point can have an enormous impact on the evolution of that substance. For example, life developed on the Earth because the Earth's mean temperature and air pressure are near the triple point of water. This allows water to exist in all three forms on the Earth's surface and serve as an environment for biochemical reactions and a universal solvent for the construction of complex macromolecules. The surface of Titan, Saturn's largest moon, has environment conditions near the triple point of methane (methane lakes, snow, rains, ice) and so methane life may have formed there. |
|
The study of the relationship between heat,
work, temperature and energy, now encompassing the general behavior of
physical system is called thermodynamics.
.. A central consideration of thermodynamics is that any physical system, whether or not it can exchange energy and material with its environment, will spontaneously approach a stable condition (equilibrium) that can be described by specifying its properties, such as pressure, temperature, or chemical composition. If the external constraints are changed (for example, if the system is allowed to expand), then these properties will generally alter. The science of thermodynamics attempts to describe mathematically these changes and to predict the equilibrium conditions of the system. The first law of thermodynamics is often called the law of the conservation of energy (actually mass-energy) because it says, in effect, that, when a system undergoes a process, the sum of all the energy transferred across the system boundary--either as heat or as work--is equal to the net change in the energy of the system. |
.. |
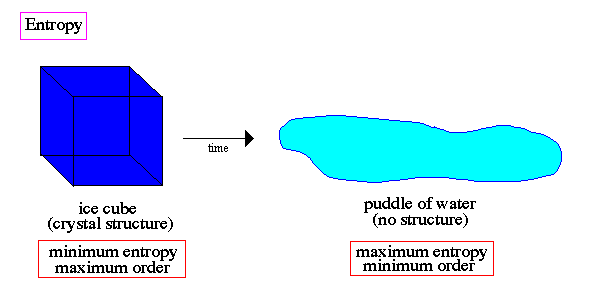
.. The second law of thermodynamics states that, in a closed system, the entropy does not decrease. Cars rust, dead trees decay, buildings collapse; all these things are examples of entropy in action, the spontaneous movement from order to disorder. There is one more influence of cosmological relationships upon macroscopic physics, which arises in connection with thermodynamics. The existence of irreversible processes in thermodynamics indicates a distinction between the positive and negative directions in time. As Clausius recognized in the 19th century, this irreversiblity reflects a quantity, first defined by him, called entropy, which measures the degree of randomness evolving from all physical processes by which their energies tend to degrade into heat. Entropy can only increase in the positive direction of time. In fact, the increase in entropy during a process is a measure of the irreversiblity of that process. |
.. |
.. The measure of entropy must be global. For example, you can pump heat out of a refrigerator (to make ice cubes), but the heat is placed in the house and the entropy of the house increases, even though the local entropy of the ice cube tray decreases. .. In a closed system, entropy never decreases. In open systems, entropy can decrease in local regions (e.g., the ice tray), but an increase in order in the open system is always paid for by a decrease in order (decrease in entropy) somewhere else (e.g., the outside room). In the growth of crystals, for example, the ordered arrangement of ions in a lattice produces heat which flows away to the nearby environment. |
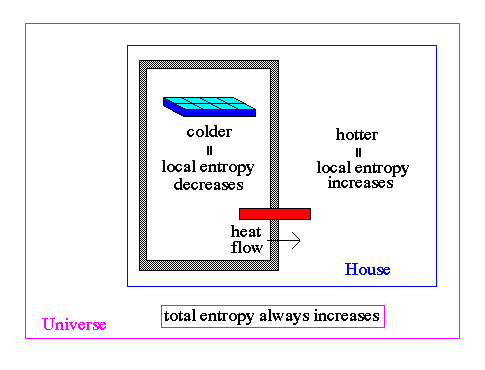
.. |
.. Classical or Newtonian physics is incomplete because it does not include irreversible processes associated with the increase of entropy. The entropy of the whole Universe always increased with time. We are simply a local spot of low entropy and our destiny is linked to the unstoppable increase of disorder in our world => stars will burn out, civilizations will die from lack of power. .. The approach to equilibrium is therefore an irreversible process. The tendency toward equilibrium is so fundamental to physics that the second law is probably the most universal regulator of natural activity known to science. .. The concept of temperature enters into thermodynamics as a precise mathematical quantity that relates heat to entropy. The interplay of these three quantities is further constrained by the third law of thermodynamics, which deals with the absolute zero of temperature and its theoretical unattainability. .. Absolute zero (approximately -273 C) would correspond to a condition in which a system had achieved its lowest energy state. The third law states that, as this minimum temperature is approached, the further extraction of energy becomes more and more difficult. |
|
Why do we perceive time as always moving forward? Why are our memories always of the past and never of the future? All the fundamental Newtonian laws are time reversible. Collisions look the same forwards or backwards. A box of gas molecules obeying Newton's laws perfectly does not have an inbuilt arrow of time. However, it is possible to show that the continual random molecular motions will cause the entire ensemble to visit and revisit every possible state of the box, much like the continual shuffling of a deck of cards will eventually reproduce any sequence. |
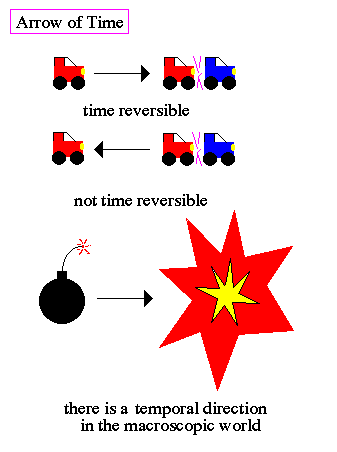
|
This ability of Nature to be divided into a
multitude of states makes it easier to understand why thermodynamical
systems move toward equilibrium, known as Poincare's theorem. If a box of
gas is in a low entropy state at one moment, it will very probably soon be
in a less ordered state since given the large number of states for it to
evolve to, most of those states are of higher entropy. So just by the laws
of chance, the box has a higher probability of becoming a higher entropy
state rather than a lower one since there are so many more possible high
entropy states.
.. Poincare's theorem claims that if every individual state has the same chance of being visited, then obviously mixed-up states are going to turn up much more often than the less mixed-up or perfectly ordered states, simply because there are many more of them. |
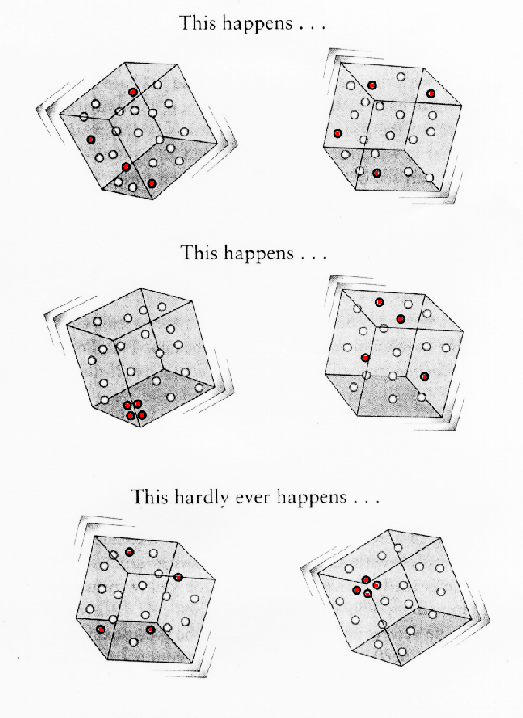
.. |
.. Thermodynamical events, such as a growing tree, are not reversible. Cracked eggs do not repair themselves. Defined by these events, time has an arrow, a preferred direction. Entropy and the arrow of time are strongly linked. Increasing entropy is in the direction of positive time. However, a study of the components to systems shows that the parts are describable in terms of time-symmetric laws. In other words, the microscopic world is ruled by time-symmetric laws, but the macroscopic world has a particular direction. |