
|
In the center of the `School of Athens' by Raphael are Aristotle and Plato, Aristotle's hand level to the Earth symbolizing his realism view of Nature; Plato's hand pointed towards the heaven symbolizing the mystical nature to his view of the Universe. This image symbols the sharp change in the meaning of how `natural philosophy' or physics will be done for the 2,200 years. |

.. |
.. Aristotle stands in the Greek philosophical tradition which asserts that nature is understandable. This tradition, opposed to the idea that nature is under the control of capricious deities which are to be appeased rather than understood, is one of the roots of science. .. Aristotle constructed his view of the Universe based on a intuitive felling of holistic harmony. Central to this philosophy was the concept of teleology or final causation. He supposed that individual objects (e.g. a falling rock) and systems (e.g. the motion of the planets) subordinate their behavior to an overall plan or destiny. This was especially apparent in living systems where the component parts function in a cooperative way to achieve a final purpose or end product. .. Aristotle also provides a good example of the way in which what one knows or believes influences the way one understands new information. His theory of motion flows from his understanding of matter as constituted of four elements: air, earth, fire, and water. Objects, being solid like earth, would tend to clump together with other solids (earth), so objects tend to fall to earth, their natural place. Thus, falling is a natural motion. |
|
..  |
.. 
|
|
.. objects to fall on the Earth |
.. fall to Earth |
.. |
.. The difficulty comes in thinking about horizontal motion. Making an object move usually has a pretty obvious cause. What's difficult is explaining why something continues in motion. |
|
..  |
.. 
|
|
.. projectiles moved |
.. "really" move |
.. |
.. Think of a spear being thrown. At first, it is not in motion, but then the thrower's arm provides an impetus which accelerates it (our vocabulary, not Aristotle's). But then, what keeps it going after it leaves the thrower's hand? It should fall to earth immediately since there's nothing obvious pushing it! .. Aristotle's answer was that as the spear flies through the air, it leaves a vacuum behind it. Air rushing in pushes the spear forward until its natural motion (falling) eventually brings it to earth. .. Aristotle also thought about the causes which start things moving. In the spear scenario, it's easy to say that the thrower's arm moves the spear, but what moves the thrower's arm? Aristotle said that another motion moved the arm (muscle contraction?) but he also realized that some earlier motion must cause the muscle to contract and that earlier motion must also have its own initiator. .. To avoid the idea that there is an infinite chain of causes, Aristotle argued that there must be an "unmoved mover," something which can initiate motion without itself being set in motion. This view was preserved by medieval Church during the Dark Ages and became the ruling paradigm. |
|
Aside from his numerous inventions, Galileo also
laid down the first accurate laws of motion for masses. Galileo realized
that all bodies accelerate at the same rate regardless of their size or
mass. Everyday experience tells you differently because a feather falls
slower than a cannonball. Galileo's genius lay in spotting that the
differences that occur in the everyday world are in incidental
complication (in this case, air friction) and are irrelevant to the real
underlying properties (that is, gravity). He was able to abstract from the
complexity of real-life situations the simplicity of an idealized law of
gravity.
.. Key among his investigations are:
Galileo also showed that objects fall with the same speed regardless of their mass. The fact that a feather falls slowly than a steel ball is due to amount of air resistance that a feather experiences (alot) versus the steel ball (very little). .. Much of this thinking dealt with objects on the Earth. Galileo didn't extend his ideas to beyond the Earth's surface, that was for an astronomer named Kepler.
|
|
Kepler
developed, using Tycho Brahe's
observations, the first kinematic
description of orbits, Newton will develop a dynamic
description that involves the underlying influence (gravity)
.. 1st law (law of elliptic orbits): Each planet moves in an elliptical orbit with the Sun at one focus. Ellipses that are highly flattened have high eccentricity. Ellipses that are close to a circle have low eccentricity. |
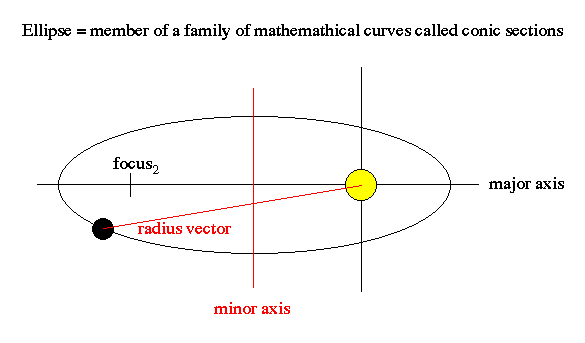
.. |
.. 2nd law (law of equal areas): a line connection the Sun and a planet (called the radius vector) sweeps out equal areas in equal times .. Objects travel fastest at the low point of their orbit, and travel slowest at the high point of their orbit. |
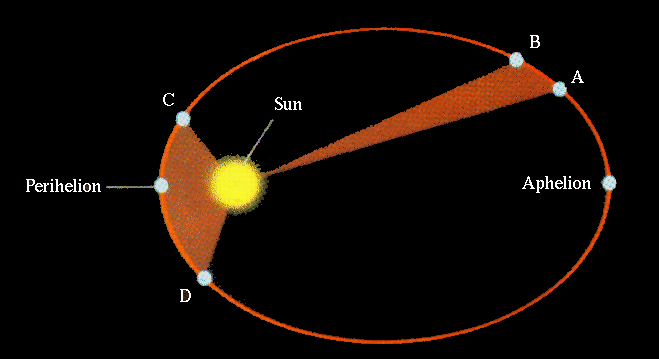
.. |
.. 3rd law (law of harmonics): The square of a planet's orbital period is proportional to its mean distance from the Sun cubed. .. The 3rd law is used to develop a "yardstick" for the Solar System, expressing the distance to all the planets relative to Earth's orbit by just knowing their period (timing how long it takes for them to go around the Sun). .. The mathematical way to describe Kepler's 3rd law is:
where the α symbol means `proportional to'. Proportions are expressions that imply there exist s some constant, k, that relates the period, P, and the radius, R, such that
.. We can determine k by expressing the formula in units of the Earth and its orbit around the S un, such that
so k is equal to one, as long as we use units of years and A.U.'s (the Astronomical Unit, i.e . the distance from the Earth from the Sun). With k=1, then kepler's 3rd law becomes
|
|
Newton
expanded on the work of Galileo to better define the relationship between
energy and motion. In particular, he developed the following concepts:
|
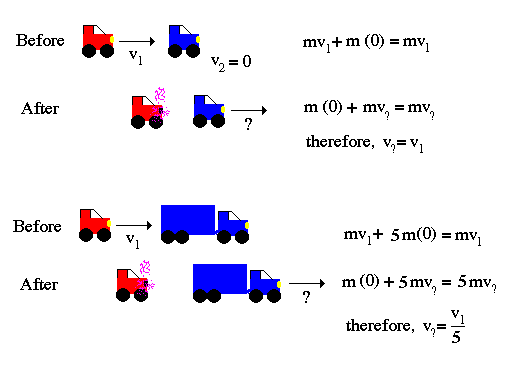
.. |
..  .. A corollary to Newton's ideas was the so called Clockwork Universe model. A concept that states that the total momentum of the Universe is conserved, interactions redistribute the momentum, but the total never changes. In this model, God only starts the clock (initial cause), then it runs by itself for the rest of time.
|
|
Example: from Newton's 1st law we know that an object travels in a straight line unless acted upon by an external force. A circular orbit is clearly not a straight line, what is the force? Newton showed that the planets are acted on by the force of gravity arising from the Sun. Each orbit is a constantly changing velocity where gravity adds a small "delta-vee" at each moment. This "delta-vee" is what produces the elliptical curvature that is the orbit. |
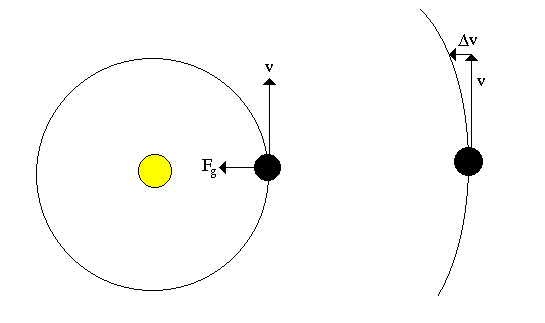
.. |
.. Example: from Newton's 2nd law when a baseball player hits a ball he applies a force, F, to the ball of mass m. Let's say he hits a tennis ball of mass of one-tenth the mass of a regular baseball (1/10m). What is the resulting acceleration? Ten times the acceleration of a regular baseball and, therefore, ten times the final velocity and ten times the distance hit. .. Example: You are trapped on a lake of ice with a sandbag. Remembering Newton's 3rd law, how do you escape? |
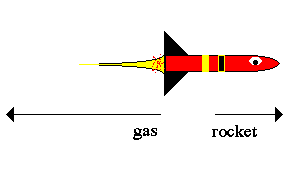
|
Galileo was the first to notice that objects are "pulled" towards the center of the Earth, but Newton showed that this same force (gravity) was responsible for the orbits of the planets in the Solar System. |
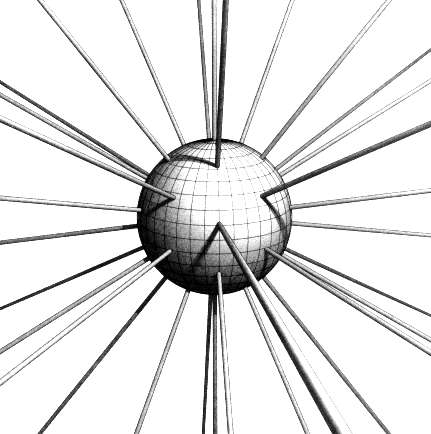
.. |
.. 
|
|
Newton went beyond his simple laws of motion and gravitation to develop a whole set of mathematics to describe and calculate orbits. Today we can this mathematics calculus. The key to calculus is the use of vectors. A vector is a quantity that has both magnitude and direction. It is typically represented symbolically by an arrow in the proper direction, whose length is proportional to the magnitude of the vector. Although a vector has magnitude and direction, it does not have position. A vector is not altered if it is displaced parallel to itself as long as its length is not changed. |
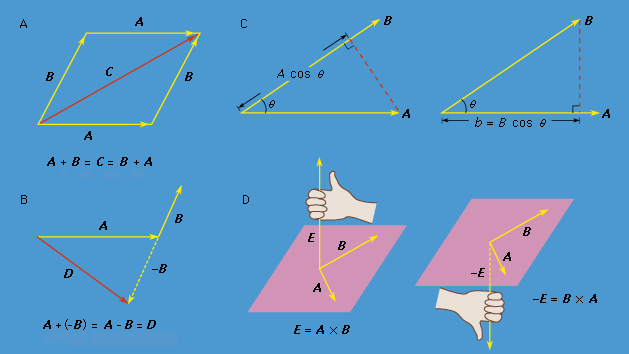
.. |
.. Because vectors are different from ordinary (i.e., scalar) quantities, all mathematical operations involving vectors must be carefully defined. If vector A is added to vector B, the result is another vector, C, written A + B = C. The operation is performed by displacing B so that it begins where A ends. C is then the vector that starts where A begins and ends where B ends. .. Vector subtraction is defined by A - B = A + (-B), where the vector -B has the same magnitude as B but the opposition direction. A vector may be multiplied by a scalar. Thus, for example, the vector 2A has the same direction as A but is twice as long. |
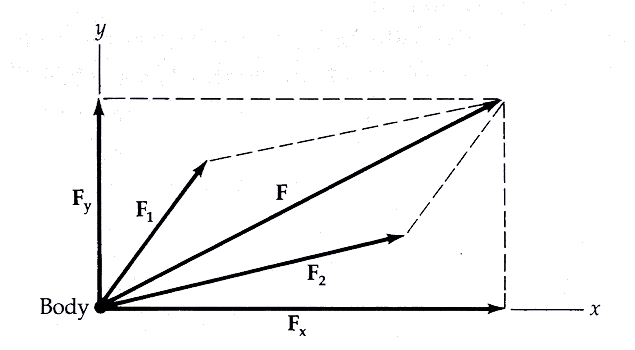
.. |
.. Newton applied vectors in terms of force. A body is added on by a vector force as shown above. Forces can be added just like vectors, so that force 1 and force 2 add together to produce the total force, F. Total force F can also be broken into components x and y that correspond to the forces in the x and y directions (for example, along a road and with gravity). .. A particle moving with constant velocity v suffers a displacement s in time t given by s = vt. The vector v has been multiplied by the scalar t to give a new vector, s, which has the same direction as v but cannot be compared to v in magnitude (a displacement of one meter is neither bigger nor smaller than a velocity of one meter per second). This is a typical example of a phenomenon that might be represented by different equations in differently oriented Cartesian coordinate systems but that has a single vector equation (for all observers not moving with respect to one another). |
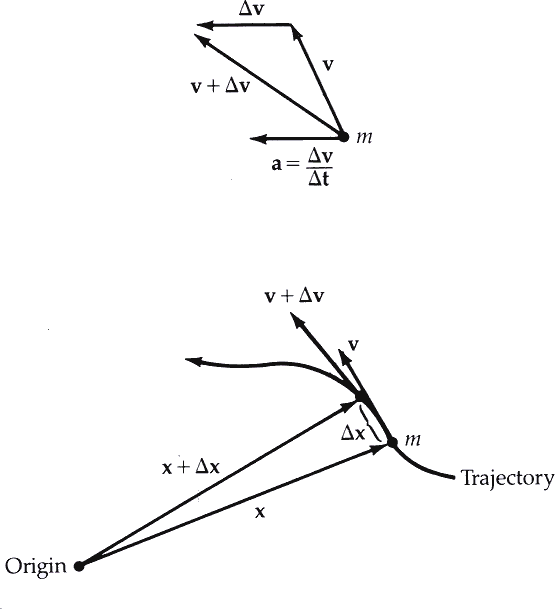
.. |
.. For a particle of mass m, a force is applied with results in an acceleration a. The acceleration changes the velocity vector by a small amount, delta v, every interval of time, delta t. This results in trajectories, a vector map of the changes in position from an origin, the vector x and the velocities, vector v. .. With vector calculus, Newton was able to develop a cosmology which included the underlying cause of planetary motion, gravity, completed the solar system model begun by the Babylonians and early Greeks. The mathematical formulation of Newton's dynamic model of the solar system became the science of celestial mechanics, the greatest of the deterministic sciences. |
|
..
dynamical description of the Solar System (Newton)
development of celestial mechanics
|
.. |
.. Although Newtonian mechanics was the grand achievement of the 1700's, it was by no means the final answer. For example, the equations of orbits could be solved for two bodies, but could not be solved for three or more bodies. The three body problem puzzled astronomers for years until it was learned that some mathematical problems suffer from deterministic chaos, where dynamical systems have apparently random or unpredictable behavior. |
.. |
Newtonian physics assumes a direct
connection between cause and effect. Electric and magnetic forces pose a
dilemma for this interpretation since there is no direct contact between
the two charges, rather there is an action
at a distance.
.. To resolve this dilemma it was postulated that there is an exchange of force carriers between charged particles. These force carriers were later identified with particles of light (photons). These particles served to transfer momentum by contact between charged particles, much like colliding cars and trucks. |
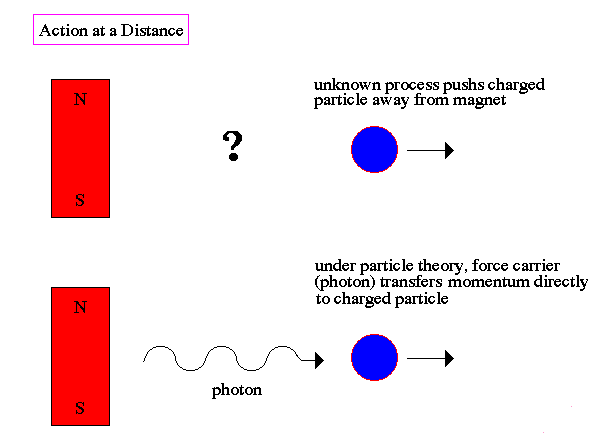
.. |
.. However, this attempt to resolve the action at a distance paradox uses a particle nature to light, when observation of interference patterns clearly shows that light has a wave-like nature. It was this dual nature to light, of both particle and wave (see wave/particle duality), that led to the revolution known as quantum physics. |