|
The fact that the Universe is rational also
implies that since our senses can deceived then they are unreliable and
possible sources of error in our understanding of the workings of Nature.
Thus, came the belief that underlying order of the Universe can be
understood by pure thought and can be expressed in mathematical form.
Thus, mathematics lies at the heart of science and is rarely questioned.
But is mathematics a human invention or does it have an independent
existence?
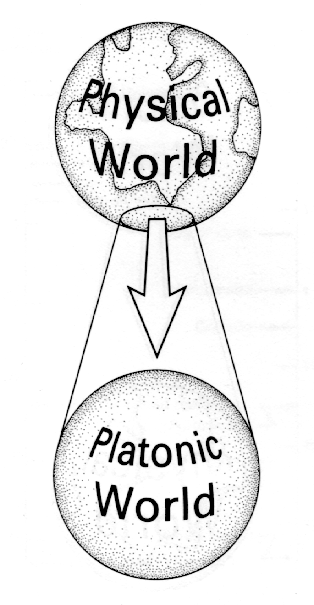
.. There exists two schools of thought. One that mathematical concepts are mere idealizations of our physical world. The world of absolutes, what is called the Platonic world, has existence only through the physical world. In this case, the mathematical world would be though of as emerging from the world of physical objects. |

.. |
.. The other school is attributed to Plato, and finds that Nature is a structure that is precisely governed by timeless mathematical laws. Plato believed that there exists an immaterial Universe of `forms', perfect aspects of everyday things such as a table, bird, and ideas/emotions, joy, action, etc. The objects and ideas in our material world are `shadows' of the forms (see Plato's Allegory of the Cave). .. This solves the problem of how objects in the material world are all distinct (no two tables are exactly the same) yet they all have `tableness' in common. There are different objects reflecting the `tableness' from the Universe of Forms. .. According to Platonists we do not invent mathematical truths, we discover them. The Platonic world exists and physical world is a shadow of the truths in the Platonic world. This reasoning comes about when we realize (through thought and experimentation) how the behavior of Nature follows mathematics to an extremely high degree of accuracy. The deeper we probe the laws of Nature, the more the physical world disappears and becomes a world of pure math. |
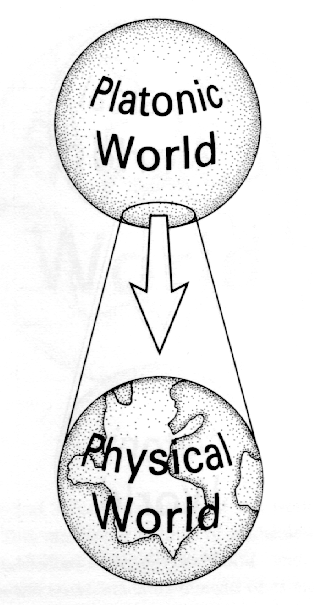
.. |
.. Mathematics transcends the physical reality that confronts our senses. The fact that mathematical theorems are discovered by several investigators indicates some objective element to mathematical systems. Since our brains have evolved to reflect the properties of the physical world, it is of no surprise that we discover mathematical relationships in Nature. .. The laws of Nature are mathematical mostly because we define a relationship to be fundamental if it can be expressed mathematically. |

|
Much of the philosophical foundation to our
mathematical sciences is due to the Pythagorean school. Pythagoras
lived in the 6th century B.C., most of the work we attribute to the
individual is more than likely a composite of work done over many
centuries by his school.
.. The Pythagorean school presented us with our first physical models, but the role of mathematics was much more dominate than it is today. For example, the Pythagoreans believe that matter was make of numbers. Not idealized numerous fragments, but actual numbers themselves. In some sense, this is an atomic theory, but with pure mathematics replacing matter objects. .. The world being composed of numbers was reached by the Pythagoreans due to their interest in gnomones. This naturally led to the development of the Pythagorean Theorem. |

.. |
.. The discovery of the Pythagorean Theorem led to a crushing blow to the Pythagorean school since it uses the idea of irrational numbers, which was repugnant to the philosophers of the time. |
|
Both Plato and Pythagoras influenced the
first logically consistent macroscopic worldview, developed by the Greeks
in the 4th century B.C. This early worldview was an extrapolation of the
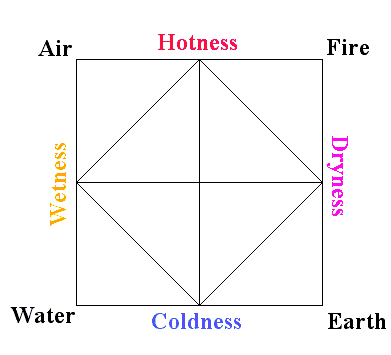
Greek theory of matter proposed by Empedocles. This theory states that all
matter in the Universe is composed of some combination of four elements:
Earth, Water, Fire, Air. These four elements arise from the working of the
two properties of hotness (and its contrary coldness) and dryness (and its
contrary wetness) upon an original unqualified or primitive matter. The
possible combinations of these two properties of primitive matter give
rise to the four elements or elemental forms.
.. Perhaps only a culture whose leaders were involved with logic and geometry would put the concepts of chemistry in such a logical and geometric form. Fire and Water are obvious opposites, and so are Earth and Air. These opposites share no common properties. There are four properties, each shared by two non-opposite elements: fire and air share the property of hotness, water and air the property of wetness, and so on. Since the four elements are two pairs of opposite elements, so also are the four properties - hotness being the opposite of coldness and wetness the opposite of dryness. Each of the four elements was held to exist in an ideal pure form, which could not actually be found on earth. The real things around us were considered impure, or mixed, forms of these four ideal elements. Thus the different airs, or gases, were the form of air mixed with different proportions of the forms of fire or water; smoke was a mixture of the forms of air and earth with some of the form of fire added. But there was an ideal or pure form of earth, air, fire, and water, and the real ones which we see and use were not ideal but of lesser purity. In other words, the real or observed different kinds of the same element are due to different degrees of the same properties. The elements could be changed into one another by removal of one property and addition of another. |
.. |
.. In a seemingly unrelated discovery, Euclid, a Greek mathematician, proved that there are only five solid shapes that can be made from simple polygons (the triangle, square and hexagon). Plato, strongly influenced by this pure mathematical discovery, revised the four element theory with the proposition that there were five elements to the Universe (earth, water, air, fire and quintessence) in correspondence with the five regular solids. |
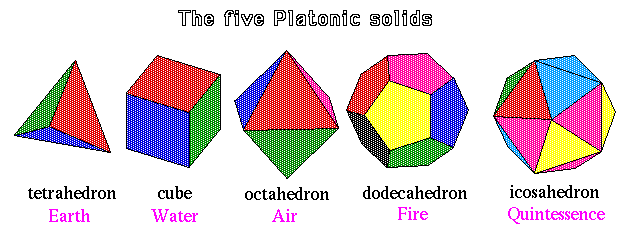
.. |
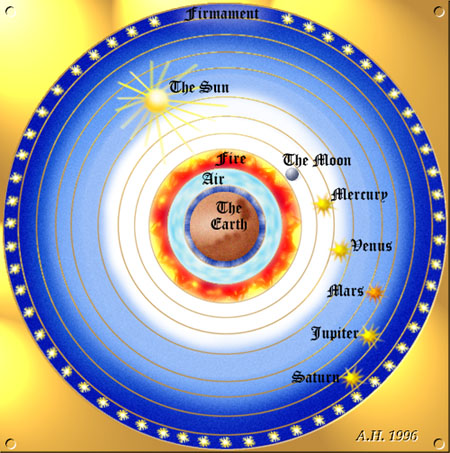
.. Elements had a natural tendency to separate in space; fire moved outwards, away from the earth, and earth moved inwards, with air and water being intermediate. Thus, each of these five elements occupied a unique place in the heavens and, thus, Plato developed the first periodic table and, at the same time, proposed the first cosmological models looked something like the following diagram: |
|
.. Mathematics went on to lead the way in many scientific and technological developments over the next 2000 years. Architecture, navigation and mechanics are all examples of core elements to our civilization that depend heavily on mathematics. By the Renaissance, mathematics was wide spread in all parts of life, including art, where the development of the golden section played a strong role in painting at the time. |
.. |
.. The historical peak of mathematics was the development of calculus by Newton as the basis for his theory of mechanics and gravitation. Calculus was so successful that the early numerological image of the Universe was replaced with a clockwork image. This clockwork model of the Universe reached its most developed form under Laplace in the late eighteenth century, who envisaged every atom in the Universe as a component in a precise cosmic mechanism. |